درخت مرکل (Merkle Tree) یکی از پایه های اساسی بلاک چین میباشد که در کارکرد آن نقش مهمی را ایفا میکند. به کمک درختهای مرکل میتوان در امنیت و با سطح بالا ساختارهای بزرگ دیتا را بررسی و تایید نمود. بلاک چینها با داشتن درخت مرکل قادر هستند مجموعههای بیکرانی از دیتا را به تایید برسانند.
ایجاد و راهاندازی درخت مرکل در بلاک چین چند نتیجه در پی خواهد داشت. یکی از این تاثیرات ایجاد امکان مقیاسگیری در بلاک چین ها میباشد. درختان مرکل علاوه بر این یک معماری بر پایه هش در بلاک چین بوجود میاورند که موجب حفظ تمامیت دیتا میگردد و بلاک چینها قادرند به سادگی تمامیت دیتا را چک نمایند. چرخدندههای نرمافزاری که درختهای مرکل را به کار میاندازند در واقع توابع هش کریپتوگرافیک میباشند. لذا اگر بخواهیم با درخت مرکل آشنا شویم در آغاز باید ببینیم این توابع هش رمزنگاری شده چه چیزی میباشند.
توابع هش کریپتوگرافیک
به عبارت ساده، تابع هش به تابعی تلقی میگردد که با آن یک دیتا در مقدار دلخواه (ورودی) را نگاشت نموده و از آن یک خروجی با مقدار مشخص میگیرند؛ یعنی تابع هش، دیتای دلخواه را بدست میگیرد و آن را با مقدار ثابت تحویل میدهد. به این جهت یک الگوریتم هشینگ (یا هش کردن) را روی دیتای ورودی پیاده مینمایند که حاصل آن یک خروجی با مقدار ثابت میباشد. این خروجی را هش نامگذاری میکنند(به همین سبب به الگوریتم آن هشینگ میگویند، زیرا از هر دیتایی هش تولید مینمایند). شمار توابع هشینگ زیاد میباشد و همگان به آنها دسترسی دارند و قادرند بسته به نیاز خود از این توابع استفاده نمایند.
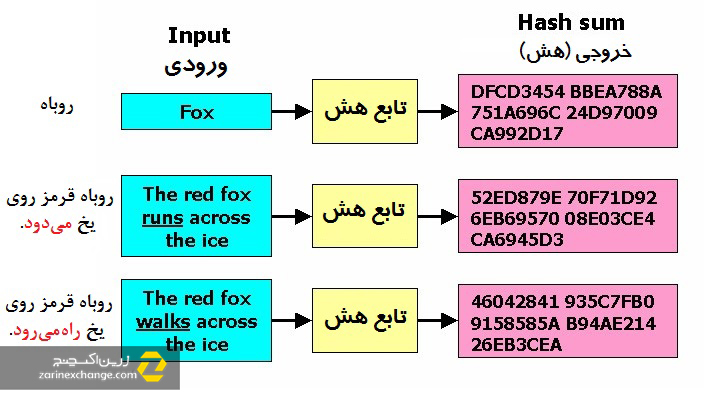
هش به دست آمده از ورودی دلخواه نه فقط طول ثابتی دارد بلکه کاملا یکتا و منحصر به ورودی میباشد. خود تابع نیز قطعی است، یعنی هر چند بار هم که تابع را روی یک ورودی اجرا نمایید خروجی همواره یک چیز خواهد بود. برای مثال اگر دیتاستهای (مجموعه دیتا) زیر را ورودی بگیریم، خروجی به دست آمده از هر کدام از ورودیها منحصر به فرد و یکتا خواهد بود. توجه داشته باشید که در نمونههای دوم و سوم، با اینکه تفاوت تنها در حد یک واژه میباشد، خروجیهای به دست آمده کاملا با هم فرق میکنند. این قابلیت تابع هشینگ بسیار مهم میباشد، زیرا به ما اجازه میدهد از دیتا «اثر انگشت» دریافت کنیم.
یک تابع هش کریپتوگرافیک. عکس از ویکی پدیا
در مثال بالا همانطور که مشاهده میکنید بعد از اجرای الگوریتم هشینگ روی دیتا، هشهای خروجی طول یکسانی در اختیار دارند. به این صورت با این شیوه میتوان اندازه کلانی از دیتا را فقط به وسیله هش خروجی شناسایی نمود. در سیستمهایی که با دیتا در اندازههای هنگفت سر و کار دارند، اندوختن و شناسایی این دیتا با خروجیهای کوچک در مقدار ثابت، به مقدار بسیار فراوانی از فضای ذخیرهسازی آنها میکاهد و کارایی این سیستمها را افزایش میدهد.
در حوزه بلاک چین، از الگوریتمهای هشینگ جهت تعیین حالت بلاک چین بهره گرفته میشود. بلاک چین ها در واقع لیستهای پیوستهای میباشند که در آنها دیتا و اشارهگر هش وجود خواهد داشت. اشارهگر هش (hash pointer) در هر بلاک به بلاک پیشین اشاره دارد و معین میکند بلاک پیشین چیست. به این صورت یک زنجیره از بلاکها به وجود میآید که یکی بعد از دیگری به هم متصل میباشند ؛ به همین سبب به این مجموعه «بلاک چین» یا زنجیره بلاکی گفته میگردد. به این صورت آنچه یک بلاک را به بلاک کنار خود وصل مینماید یک اشارهگر هش میباشد. هر اشارهگر هش دارای دو قسمت میباشد. یکی آدرس بلاک پیشین و دیگری هش برگرفته از دیتای موجود در بلاک پیشین. در این شیوه هر هش که خروجی دیتای بلاک قبلی میباشد، نشانگر حالت کل بلاک چین نیز میباشد چراکه این هش نتیجه تمام دیتاهای هش شده بلاکهای قبلی است. این هش خروجی (اگر الگوریتم SHA-256 باشد) شبیه چنین چیزی میباشد:
b09a57d476ea01c7f91756adff1d560e579057ac99a28d3f30e259b30ecc9dc7
این هش در واقع اثر انگشتی از وضعیت کلی بلاک چین تا قبل از خود میباشد. لذا حالت بلاک چین تا قبل از بلاک تازه (و هش گرفتن از آن) ورودی بشمار میرود و هش به دست آمده از آن خروجی میباشد. میتوان بدون کمک درخت مرکل از هشهای رمزنگاری شده بهرمند شد اما با این شیوه کارایی به شدت کاهش میابد و امکان مقیاس پذیری از بین خواهد رفت. بهره از هش جهت ذخیرهسازی دیتا در بلاک به شکل سری، کاری بسیار دشوار و زمانبر میباشد.
با این همه همانطور که در ادامه مشاهده خواهید کرد، درختان مرکل خطر ناچیزی برای تمامیت دیتا بوجود میاورند و به کمک اثبات مرکل (Merkle proof) میتوان دیتا را در سرتاسر درخت نگاشت نمود (نقشه آن را تهیه نمود).
درخت مرکل و اثبات مرکل
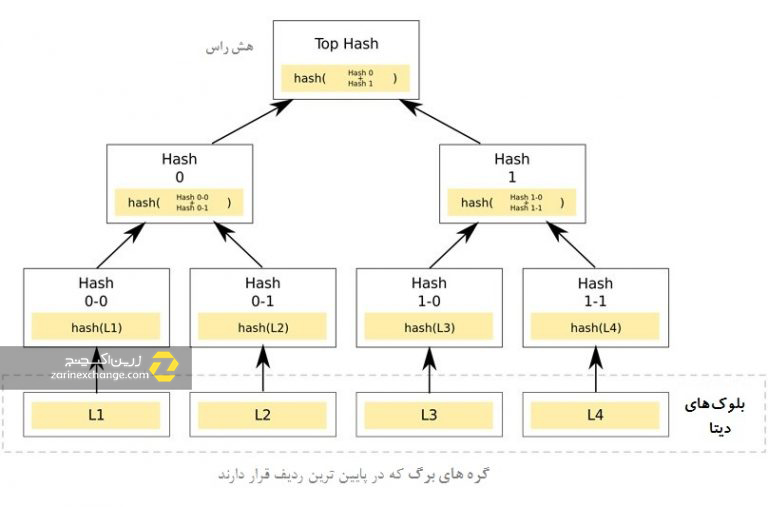
نام درخت مرکل برگفته از رالف مرکل (Ralph Merkle) میباشد. دانشمندی که در سال ۱۹۷۹ این مفهوم را معرفی کرد. درختهای مرکل در واقع ساختارهایی از دیتا به شکل درخت میباشند که در آنها، هر گره غیر – برگ، هش گرههای زیرشاخهی خود میباشد. گرههای برگ، پایینترین ردیف گره در درخت میباشند. امکان دارد ابتدا درک درخت مرکل سخت به نظر برسد ولی اگر به تصویر زیر دقت داشته باشید (که یکی از شکلهای رایج میباشد) میبینید که درک آن بسیار ساده است.
نمونهای از یک درخت مرکل باینری، عکس از ویکیپدیا
در شکل بالا باید توجه داشته باشید که گرههای غیر برگ یا همان شاخههای سمت چپ (Hash 0-0 و Hash 0-1) هشهای زیرشاخه خود یعنی L1 و L2 میباشند. یک ردیف بالاتر، شاخه Hash 0، هش دو زیرشاخه خود یعنی شاخههای Hash 0-0 و Hash 0-1 میباشد.
نمونه بالا در واقع یک درخت مرکل ساده است. این رایجترین نمونه به اسم درخت مرکل باینری (binary) شناخته میگردد. همانطور که مشاهده میکنید یک هش راس وجود دارد که هش همهی درخت میبادش. این هش را با اسم روت هش یا هش ریشه میشناسند. درخت مرکل یک ساختار دیتا میباشد که قادر است n شاخه داشته باشد و همهی آن را با یک هش بیان نماید.
با استفاده از ساختار درخت مرکل میتوان هر مقدار دیتای دلخواه را با کارآمدی بالا نگاشت نمود و بروز هرگونه تغییر در دیتا را به سهولت شناسایی نمود . اساس این مفهوم به اثبات مرکل گره خورده که به واسطه آن میتوان درستی هشینگ دیتا را از پایین تا راس درخت تایید نمود و قرارگیری آن در جای صحیح را بررسی کرد؛ بدون اینکه نیاز باشد همه هشها را چک نماییم. به همین جهت به واسطه اثبات هش میتوان تنها با چک کردن یک زیرمجموعه کوچک از هشها (به جای همهی دیتاست) دریافت که یک دیتا با روت هش (Hash Root) خود همخوانی دارد یا خیر.
تا هنگامی که روت هش علنی و معتبر باشد، هر فردی که قصد داشته باشد یک دیتابیس را از نظر ارقام کلیدی ارزیابی نماید، قادر سات با یک اثبات مرکل، درستی جایگاه و تمامیت یک تکه دیتا را در دیتابیس دارای روت مشخص چک نماید. چنانچه روت هش در دسترس باشد، میتوان درخت هش را از هر منبعی (بدون نیاز به اطمینان به آن) دریافت کرد و هر بار همزمان با دانلود یک شاخه از درخت، تمامیت دیتا را چک نمود؛ حتی اگر تمام درخت در دسترس نباشد.
یکی از اصلی ترین مزایای ساختار درخت مرکل این میباشد که میتوان با یک مکانزیم هشگیری، صحت مجموعههای دیتا در مقدار دلخواه را مشخص نمود؛ از دیتاهای خیلی کوچک گرفته تا دیتاستهای بسیار درشت. قابلیت برجسته درخت مرکل این میباشد که ستهای بزرگی از دیتا را به قسمت های کوچک و قابل اداره تقسیم مینماید. به این صورت حتی اگر اندازهی دیتای کلی خیلی بزرگ باشد، چک کردن تمامیت آن همچنان ساده خواهد بود.
میتوان از روت هش به عنوان اثرانگشت کل یک دیتاست بهرمند شد. برای مثال میتوان با آن کل یک دیتابیس یا وضعیت کلی یک بلاک چین را بیان کرد. در ادامه میبینیم که سیستمهایی مانند بیت کوین چگونه از درخت مرکل استفاده کرده اند.
درخت مرکل در بیت کوین
تابع هش کریپتوگرافیک به کار گرفته شده در بیت کوین را «الگوریتم SHA-256 » نامگذاری میکنند. این اسم مخفف عبارت «الگوریتم هشینگ امن» (Secure Hashing Algorithm) میباشد که خروجی آن طول ثابتی به مقدار ۲۵۶ بیت دارد. تابع بنیادی درخت مرکل در بیت کوین در آغاز تراکنشها را در بلاک ذخیره نموده و در انتهای آنها را از بلاک بیرون میکشد.
همانگونه که قبل تر گفتیم، در بلاک چین بلاکها به واسطه هشها به هم وصل میباشند و این هشها برگرفته از بلاک پیشین هستند. در بیت کوین، هر بلاک دارای تعدادی تراکنش و یک سربلاک یا بلاک هِدِر (block header) میباشد. سربلاک دارای قسمت های زیر است:
- شماره ورژن بلاک
- هش بلاک پیشین
- تایماستمپ یا برچسب زمانی
- سختی استخراج مورد نظر
- نانس
- روت هش مرکل
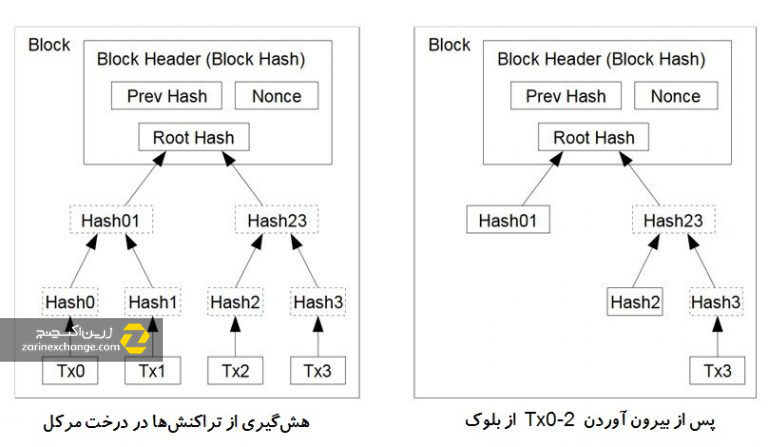
عکس زیر که برگرفته از وایت پیپر بیت کوین میباشد ؛ و بیان میکند که چگونه درخت مرکل در هر بلاک فعالیت دارد.
در آغاز ماینرها، تراکنشها را در بلاک قرار میدهند سپس کار درخت مرکل آغاز میشود. به این صورت که ابتدا از تراکنشها هش گرفته شده و این روند هشگیری در نهایت به ریشه مرکل (Merkle root) یا همان روت هش میرسد که در سربلاک ذخیره میگردد. این ساختار چند مزیت مهم دارد. نخست اینکه همانطور که در وایت پیپر بیت کوین آمده، این ساختار باعث به وجود آمدن گرههای «تایید پرداخت ساده» (SPV) میشود. این گرهها به «کلاینتهای سبکوزن» (lightweight clients) مشهورند. کلاینت سبک وزن مجبور نیست همه بلاک چین بیت کوین را دانلود کند؛ تنها کافی است سربلاکهای بلندترین زنجیره بیت کوین را بگیرد. به این منظور، گرههای SPV باید در گرههای همتای خود جستجو کنند تا زمانی که مطمئن شوند سربلاکهایی که در اختیار دارند مربوط به بلندترین زنجیره هستند. هر گره SPV میتواند وضعیت یک تراکنش را تعیین کند. برای این کار گره با استفاده از اثبات مرکل، تراکنش را در یک درخت مرکل مشخص نگاشت میکند. روت هش این درخت مرکل در سربلاکی قرار دارد که بخشی از بلندترین زنجیره است.
از سوی دیگر، پیادهسازی درختان مرکل در بیت کوین امکان هرس کردن بلاک چین را فراهم میکند که همان بیرون کشیدن تراکنشها از بلاک است. با این کار در فضای ذخیرهسازی صرفهجویی میشود. دلیل این کار آن است که تنها روت هش یک درخت مرکل در سربلاک ذخیره میشود، بنابراین میتوان شاخههای غیرضروری درخت مرکل را در بلاکهای پیشین هرس کرد زیرا تنها به بخشی از درخت مرکل برای اثبات مرکل مورد نیاز است و میتوانیم باقی آن را دور بریزیم.
درخت مرکل در دیگر بلاک چین ها و سیستمها
بیت کوین نخستین بلاک چینی بود که از درخت مرکل بهره گرفت. پس از بیت کوین، بلاک چینهای دیگر به سراغ پیادهسازی ساختارهای مشابهی از درخت مرکل رفتند و حتی برخی از آنها در پی نسخههای پیچیدهتر بودند. افزون بر این، بهرهگیری از درخت مرکل به بلاک چینها محدود نشد و به سیستمهای گوناگون دیگر نیز راه پیدا کرد.
اتریوم که در کنار بیت کوین شناخته شدهترین رمز ارز جهان است، بزرگترین نمونه استفاده از درخت مرکل پس از بیت کوین است. ساختار درخت مرکلی که اتریوم اجرا کرده با نسخه بیت کوین تفاوت دارد. دلیل آن این است که اتریوم یک سیستم تورینگ کامل (turing-complete) است و پلتفرمی برای طراحی کارکردها و اپلیکیشنهای پیچیدهتر است. به همین خاطر نسخه درخت مرکل به کار رفته در اتریوم پیچیدهتر است. این نسخه، درخت مرکل پاتریشیا (Merkle Patricia Tree) نام دارد و در حقیقت ۳ درخت مرکل جداگانه است که برای سه کار متفاوت استفاده میشوند.
درخت مرکل یکی از اجزای اساسی سیستمهای کنترل نسخه توزیع شده است و سیستمهایی مانندGit و IPFS از آن بهره بردهاند. توانایی درخت مرکل در تایید بیدردسر تمامیت دیتای مشترک میان کامپیوترها با فرمت P2P آن را به یک ابزار غیرقابل ارزشگذاری برای چنین سیستمهایی تبدیل کرده است.
درخت مرکل یکی از اجزای تشکیل دهنده بلاک چین است و وجود آن باعث شده این سیستمها با تغییرناپذیری قابل اثبات و حفظ تمامیت تراکنش به کار خود ادامه دهند. برای سر درآوردن از مفاهیم بنیادین رمز ارزها، درک نقشی که درختان مرکل در شبکههای توزیع شده بازی میکنند و شناخت تکنولوژی زیربنای توابع هش کریپتوگرافیک ضروری است، چرا که این سیستمها در حال بزرگتر شدن و پیچیدهتر شدن هستند.